Tarjan 强连通分量学习笔记

发表于 更新于 分类于 ， 阅读次数： Disqus：

鸽了好久

概念

强连通图：指的是一张有向图，其中从任意一个节点出发，都可达到该图的所有节点。

强连通分量：指的是有向图的一种子图，满足该子图为强连通图，且这个子图是 极大 的，即对于一幅图 \(G\) 的强连通分量 \(G_0\)，我们无法找到一副子图 \(G_1\) 为强连通图，且满足 \(G_0 \subsetneqq G_1 \subseteq G\)

Tarjan

时间戳

对于一张图，我们可以使用 Tarjan 算法求出这张图的强连通分量。

Tarjan 算法引入了一个概念：时间戳，即对一张图进行 DFS 时经过每个点的顺序。用 \(\text{dfn}_i\) 表示。

对于下面这幅图：

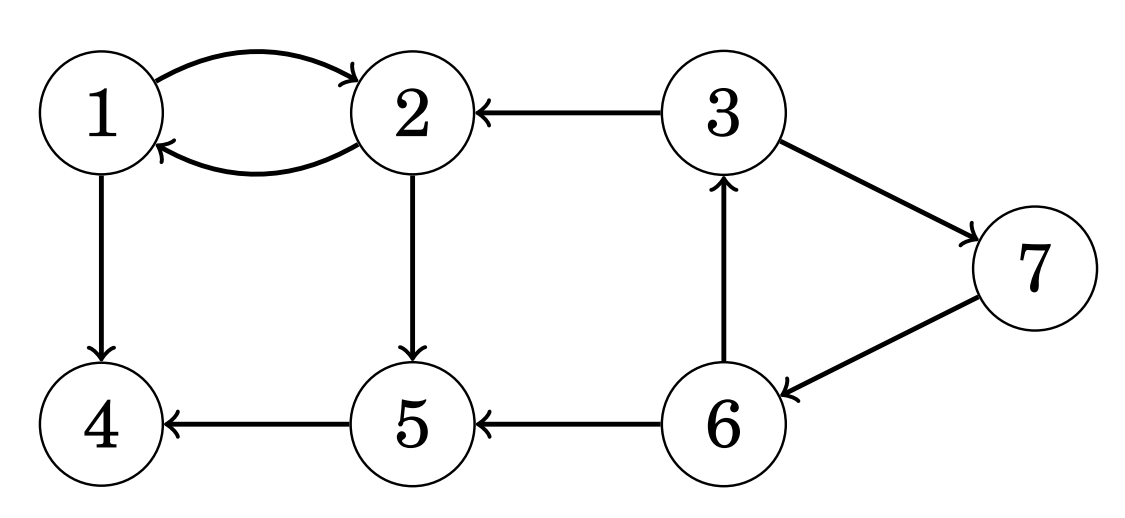
该图对应的时间戳为：

\[ \begin{align} \text{dfn}_1 = 1 \quad \text{dfn}_2 = 2 \quad \text{dfn}_5 = 3 \quad \text{dfn}_4 = 4 \\ \text{dfn}_3 = 5 \quad \text{dfn}_7 = 6 \quad \text{dfn}_6 = 7 \end{align} \]

边的分类

我们可以很容易地看出，对于一个环，环中的节点都属于同一个强连通分量。

Tarjan 则是通过改编 DFS 来找“环”的一种算法。

于是我们可以基于时间戳将边分个类。首先我们定义搜索所经过的边构成了一颗搜索树（或森林）。

于是对于有向边 \((x, y)\) 我们可以得到下列几种边：

  • 树枝边：即为搜索时经过的边，反映在搜索树上即为 \(x\) 为 \(y\) 的父节点；

  • 前向边：即为在搜索树中祖先节点指向孙子节点，即 \(x\) 为 \(y\) 的祖先；

  • 后向边：即为在搜索树中孙子节点指向祖先节点，即 \(y\) 为 \(x\) 的祖先；

  • 横插边：即为除了上述三种情况的边，此时必满足 \(\text{dfn}_y < \text{dfn}_x\)。

下面这幅图很好地阐释了四种边的类型（摘自《算法竞赛进阶指南》）。加粗的边为树枝边，其余边则取第一个汉字：

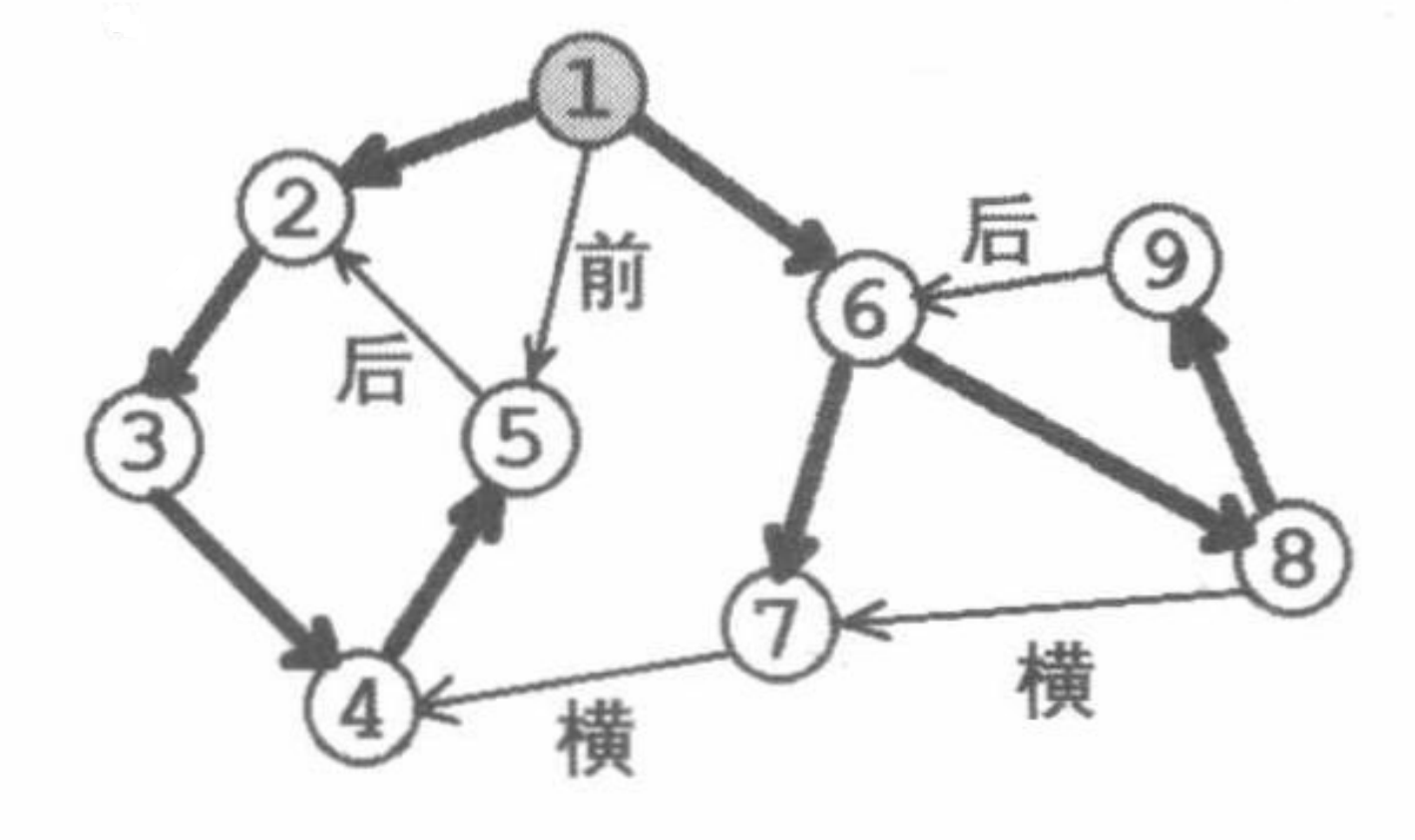
求解强连通分量

对“环”的理解

对于“环”有影响的有两种边：后向边和横插边。

为了求后向边和横插边，我们可以维护一个栈，在访问 \(x\) 节点时，存储以下信息：

  • 搜索树上 \(x\) 的祖先节点；

  • 已经访问过的，且可通过一条路径就到达 \(x\) 祖先节点的节点。

对于节点 \(y\)，只要 \(y\) 有一条路径到 \(x\) 的祖先，且存在一条 \(x \rightarrow y\) 的横插边，显然 \(x\)、\(x\) 的祖先和 \(y\) 形成了一个环，属于同一个强连通分量。

追溯值

接下来我们需要看怎么求树枝边和横插边。

这时我们可以引入一个追溯值 \(\text{low}_i\)，表示由节点 \(i\) 开始搜索所能到达的点中，在搜索树上是 \(i\) 的祖先的节点中最小的时间戳。

于是我们可以对节点 \(x\) 进行下列操作：

  1. 当节点 \(x\) 第一次被访问时，把 \(x\) 入栈，初始化 \(\text{low}_x = \text{dfn}_x\)；

  2. 扫描从 \(x\) 出发的边 \(x \rightarrow y\)：

    1. 若 \(y\) 没访问过，则说明 \(y\) 是 \(x\) 的树枝边，递归访问 \(y\)，从 \(y\) 回溯后，令 \(\text{low}_x = \min \{ \text{low}_x, \text{low}_y \}\)；

    2. 若 \(y\) 被访问过并且 \(y\) 在栈中，则令 \(\text{low}_x = \min \{ \text{low}_x, \text{dfn}_y \}\)。

  3. 从 \(x\) 回溯之前，判断是否有 \(\text{low}_x = \text{dfn}_x\)。若成立，则不断从栈中弹出节点，直至 \(x\) 出栈。

显然在第三步中当 \(\text{low}_x = \text{dfn}_x\) 时，栈顶到栈中 \(x\) 之间必有节点都通过树枝边或横插边连向 \(x\)，且其中的其余节点有至少一条路径连线该节点。即这些节点构成一个环，属于同一个强连通分量。此时只需在出栈的时候记录其中节点属于同一强连通分量即可。

Tarjan 的时间复杂度为 \(O(n + m)\)，是一个非常高效的算法。

代码模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void tarjan(int x) {
    dfn[x] = low[x] = ++num;
    sta.push(x);
    ins[x] = 1;
    for (int each : e[x]) {
        if (!dfn[each]) {
            tarjan(each);
            low[x] = std::min(low[x], low[each]);
        } else if (ins[each]) {
            low[x] = std::min(low[x], dfn[each]);
        }
    }
    if (dfn[x] == low[x]) {
        cnt++;
        int y;
        do {
            y = sta.top();
            sta.pop();
            ins[y] = 0;
            c[y] = cnt, scc[cnt].push_back(y);
        } while (x != y);
    }
}

缩点

求解完强连通分量可选择将强连通分量缩成一个点以便计算。

代码模板见下：

1
2
3
4
5
6
for (int i = 1; i <= n; i++) {
    for (int each : e[i]) {
        if (c[i] == c[each]) continue;
        ec[c[i]].push_back(c[each]);
    }
}

例题

洛谷 P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

本题仅需要将强连通分量缩点，统计出出度为 \(0\) 的点的个数。若个数为 \(1\)，答案则为该连通分量内节点个数，否则没有明星牛。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
#include <stack>

const int MAXN = 10000;

int n, m;
std::vector<int> e[MAXN + 1];
int dfn[MAXN + 1], low[MAXN + 1], num = 0, cnt = 0;
std::stack<int> sta;
int ins[MAXN + 1], c[MAXN + 1];
std::vector<int> scc[MAXN + 1];
std::vector<int> ec[MAXN + 1];

void tarjan(int x) {
    dfn[x] = low[x] = ++num;
    sta.push(x);
    ins[x] = 1;
    for (int each : e[x]) {
        if (!dfn[each]) {
            tarjan(each);
            low[x] = std::min(low[x], low[each]);
        } else if (ins[each]) {
            low[x] = std::min(low[x], dfn[each]);
        }
    }
    if (dfn[x] == low[x]) {
        cnt++;
        int y;
        do {
            y = sta.top();
            sta.pop();
            ins[y] = 0;
            c[y] = cnt, scc[cnt].push_back(y);
        } while (x != y);
    }
}

int main() {
    std::cin >> n >> m;

    for (int i = 1, a, b; i <= m; i++) {
        scanf("%d%d", &a, &b);
        e[a].push_back(b);
    }

    memset(dfn, 0, sizeof(dfn));
    for (int i = 1; i <= n; i++) {
        if(!dfn[i]) tarjan(i);
    }

    for (int i = 1; i <= n; i++) {
        for (int each : e[i]) {
            if (c[i] == c[each]) continue;
            ec[c[i]].push_back(c[each]);
        }
    }

    int counts = 0, pos = 0;
    for (int i = 1; i <= cnt; i++) {
        if (ec[i].size() == 0) {
            counts++;
            pos = i;
        }
    }

    if (counts == 1) std::cout << scc[pos].size() << std::endl;
    else std::cout << "0" << std::endl;

    return 0;
}