「NOI 2001」炮兵阵地 - 状压 DP
题意描述
司令部的将军们打算在 \(N \times M\) 的网格地图上部署他们的炮兵部队。一个 \(N \times M\) 的地图由 \(N\) 行 \(M\) 列组成,地图的每一格可能是山地(用 H 表示),也可能是平原(用 P 表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
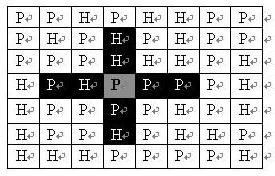
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
数据范围:\(N \leq 100\),\(M \leq 10\)