题意描述
洛谷链接
LibreOJ 链接
司令部的将军们打算在 \(N \times M\)
的网格地图上部署他们的炮兵部队。一个 \(N
\times M\) 的地图由 \(N\) 行
\(M\)
列组成,地图的每一格可能是山地(用 H 表示),也可能是平原(用 P
表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
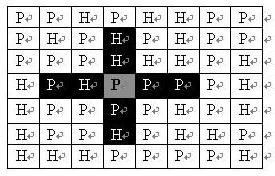
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
数据范围:\(N \leq 100\),\(M \leq 10\)
解题思路
显然这道题是状压 DP。
对于这道题,由于放置本行的炮兵和上两行都有关,于是我们可以定义状态为:
\[
f_{i, j, k} \quad i \in [1, n] \cap \mathbb{Z}, j \in S_j, k \in S_k
\]
其中 \(i\) 表示遍历到第 \(i\) 行,\(j\) 表示该行状态,\(k\) 表示上一行状态。其中 \(S_j\),\(S_k\) 分别表示 \(j\) 和 \(k\) 的合法情况的集合。
于是我们可以很容易地推出下列状态转移方程:
\[
f_{i, j, k} = \max \limits_{l \in S_l} \{ f_{i - 1, k, l} + \text{cnt}_j
\} \quad i \in (1, n] \cap \mathbb{Z}, j \in S_j, k \in S_k
\]
其中 \(l\) 为上两行的状态,\(S_l\) 同理。\(\text{cnt}_j\) 表示的是在第 \(j\) 行放置的炮兵数。
对于该题,由于空间有限,我们可以先将合法的状态存起来,离散化一下,遍历的时候就直接用离散化过的数据遍历即可。时间复杂度为
\(O(n(2^m)^3) =
O(n8^m)\),空间复杂度远小于时间复杂度。
代码演示
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
| #include <cstring>
#include <iostream>
const int MAXN = 100, MAXM = 10;
int n, m;
char board[MAXN + 1][MAXM + 1];
int f[MAXN + 1][30 * MAXM + 1][30 * MAXM + 1];
int s[100 * MAXM + 1], len = 0;
void getSet() {
s[0] = 0;
for (int i = 0; i < (1 << m); i++) {
if (i & (i << 1)) continue;
if (i & (i << 2)) continue;
s[++len] = i;
}
}
inline int count(int x) {
int cnt = 0;
for (int i = 0; i < m; i++) {
if ((s[x] >> i) & 1) {
cnt++;
}
}
return cnt;
}
inline bool check(int pos, int now) {
for (int i = 0; i < m; i++) {
if ((board[pos][i + 1] == 'H') && ((s[now] >> i) & 1)) {
return false;
}
}
return true;
}
inline void init() {
getSet();
memset(f, -0x3f, sizeof(f));
f[0][0][0] = 0;
for (int i = 0; i <= len; i++) {
if (check(1, i)) {
f[1][i][0] = count(i);
}
}
}
inline void dp() {
init();
for (int i = 2; i <= n; i++) {
for (int j = 0; j <= len; j++) {
if (check(i, j)) {
for (int k = 0; k <= len; k++) {
if (check(i - 1, k) && (s[j] & s[k]) == 0) {
for (int l = 0; l <= len; l++) {
if (check(i - 2, l) && (s[j] & s[l]) == 0) {
f[i][j][k] = std::max(f[i][j][k], f[i - 1][k][l] + count(j));
}
}
}
}
}
}
}
}
inline int getAns() {
int ans = 0;
for (int i = 0; i <= len; i++) {
for (int j = 0; j <= len; j++) {
ans = std::max(ans, f[n][i][j]);
}
}
return ans;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
std::cin >> board[i][j];
}
}
dp();
std::cout << getAns() << std::endl;
return 0;
}
|
