网络流学习笔记

网络流是一个图论中很大的知识点，这里只涉及部分内容。本篇只涉及最大流、最小割和费用流的相关知识。

概念

一张有向图 \(G = (V, E)\)，对于每条边 \((u， v) \in E\) 都有一个权值 \(c(u, v) > 0\)，称为边的 容量。且对于图上没有的边 \((u， v) \notin E\)，\(c(u, v) = 0\)，则这张图叫做一个 网络，图中有两个特殊的点 \(s \in V\) 和 \(t \in V\)，这两个点称为 源点 和 汇点。

我们设 \(f(u, v)\) 是一个两个自变量均为节点（\(u \in V, v \in V\)）的函数，且满足下列性质：

• \(f(u, v) \le c(u, v)\)（容量限制）
• \(f(u, v) = -f(v, u)\)（斜对称）
• \(\forall u \in \complement_V\{s, t\}, \sum_{(u, x) \in E}{f(u, x)} = \sum_{(x, v) \in E}{f(x, v)}\)（流量守恒）

则我们称 \(f(u, v)\) 为网络的 流函数。对于 \((u, v) \in E\)，\(f(u, v)\) 称为这条边的 流量。\(c(u, v) - f(u, v)\) 称为这条边的 剩余流量。\(\sum_{(s, u) \in E}{f(s, u)}\) 则被称为整个网络的流量。

像下图就是一张网络。在边上标记的数字为 \(f(u, v) / c(u, v)\)。

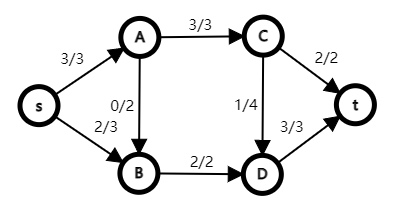
通过流函数性质我们可以发现：除了源点和汇点外，任何节点都不储存流，且流入总量等于流出总量。于是可以形象化地表述为：在不超过容量限制地前提下，流从源点经过网络流向汇点。

最大流

我们把拥有最大流量的网络流称为最大流，即为 \(\sum_{(s, u) \in E}{f(s, u)}\) 最大化。如《概念》上图所示。解决最大流问题最常用 Edmonds-Karp 和 Dinic 两种算法。

Edmonds-Karp 增广路算法（EK 算法）

在介绍 EK 算法前，我们需要先了解增广路。

在原图 \(G\) 中若一条从源点到汇点的路径上所有边的剩余容量都大于 \(0\)，这条路被称为 增广路。

EK 算法则是不停地使用 BFS 算法求出增广路，然后扩大该路的流量，将流量计入答案。直至网络中不存在增广路为止。

方法是每次从源点开始 BFS，寻找 \(f(u, v) < c(u, v)\) 的边，任意找到一条从 \(s\) 到 \(t\) 的路径，同时存储最小剩余容量 \(\text{minF}\)，于是网络流量可增加 \(\text{minF}\)。

同时注意由于斜对称性质，需要给每条边加反流量，即 \(f(v, u) = -f(u, v)\)。加反边可利用流函数的特性找到更优的增广路，找到多条增广路来抵消不优的增广路，从而得到最优的增广路。形象化地话就看下图（图片引用自 OI Wiki）：

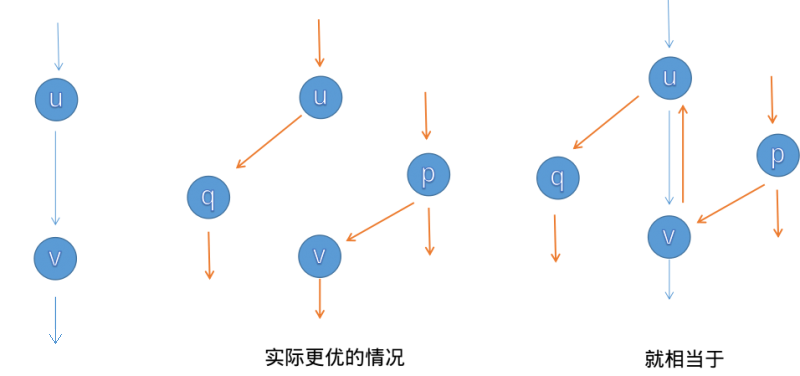
这种算法的最差时间复杂度为 \(O(nm^2)\)。

然而直接求最大流问题，用得最多，且相对高效的算法是 Dinic 算法。

Dinic 算法

每次 BFS 只找一条增广路属实浪费，于是衍生出来了 Dinic 算法。

我们需要直到一个概念：在任意时刻，网络中所有节点以及剩余容量大于 \(0\) 的边组成的子图叫做 残量网络。

Dinic 算法的核心就是通过 BFS 构建出的 分层图，然后使用 DFS 在分层图上找增广路，在回溯时实时更新流量，直到找不到增广路为止。最后再使用 BFS 构建分层图，如此往复，直到构建不出分层图即得出答案。

Dinic 可进行当前弧优化。即对于每个点，它的某个出边在增广后就没用了。于是我们在下一次 DFS 的时候就可以直接从下一条边遍历即可。

代码实现如下：

struct Node {
    std::vector<struct Edge> e;
    std::vector<struct Edge>::iterator c;
    int l;
};

struct Edge {
    Node *s, *t;
    int c, f, r;

    Edge(Node *s, Node *t, int c, int r) : s(s), t(t), c(c), f(0), r(r) {}
};

inline void addEdge(Node *s, Node *t, int c) {
    s->e.emplace_back(s, t, c, t->e.size());
    t->e.emplace_back(t, s, 0, s->e.size() - 1);
}

struct Dinic {
    std::vector<Node> &nodes;

    Dinic(std::vector<Node> &nodes) : nodes(nodes) {}

    bool level(Node *s, Node *t, int n) {
        for (int i = 1; i <= n; i++) {
            nodes[i].c = nodes[i].e.begin();
            nodes[i].l = 0;
        }

        std::queue<Node *> q;
        q.push(s);

        s->l = 1;

        while (!q.empty()) {
            Node *u = q.front();
            q.pop();

            for (auto &[u, v, c, f, r] : u->e) {
                if (f < c && !v->l) {
                    v->l = u->l + 1;
                    if (v == t) return true;
                    else q.push(v);
                }
            }
        }

        return false;
    }

    int find(Node *s, Node *t, int limit = INT_MAX) {
        if (s == t) return limit;

        for (auto &e = s->c; e != s->e.end(); e++) {
            auto &[u, v, c, f, r] = *e;
            if (f < c && v->l == s->l + 1) {
                int flow = find(v, t, std::min(limit, c - f));
                if (flow) {
                    f += flow;
                    v->e[r].f -= flow;
                    return flow;
                }
            }
        }

        return 0;
    }

    int operator()(int s, int t, int n) {
        int res = 0;
        while (level(&nodes[s], &nodes[t], n)) {
            int f;
            while ((f = find(&nodes[s], &nodes[t])) > 0) res += f;
        }
        return res;
    }
};

使用最大流算法也可以解决二分图最大匹配问题。设二分图的两个独立点集 \(A\)、\(B\)，我们只需要将源点向 \(A\) 中的点连接容量为 \(1\) 的边，将 \(B\) 中的点向汇点连接容量为 \(1\) 的边，同时将 \(A\)、\(B\) 之间的边容量设为 \(+\infty\)。最后跑一遍 Dinic 得到的结果即为最大匹配数。

Dinic 的时间复杂度为 \(O(n^2m)\)，处理二分图最大匹配时复杂度甚至可达 \(O(m \sqrt{n})\) 吊打匈牙利算法，是一种非常高效的算法。

最小割

对于一个网络 \(G = (V, E)\)，源点和汇点分别为 \(s\) 与 \(t\)。若有一边集 \(E' \subseteq E\) 且这张图删掉 \(E'\) 后 \(s\) 与 \(t\) 将不连通，则称 \(E'\) 为这个网络的 割。边的容量总和最小的割则称为这个网络的 最小割。

最小割有一个很重要的定理：任何一个网络中的最大流量等于最小割中边的容量之和，即“最大流 \(=\) 最小割”。这称之为最大流最小割定理。

证明：我们假设“最小割 \(<\) 最大流”，则删掉最小割中的边后，由于网络流量未最大化，我们仍然能找到一条从 \(s\) 到 \(t\) 的增广路，故假设不成立。于是满足“最小割 \(\ge\) 最大流”。而删去最大流后在残量网络中我们无法找到从 \(s\) 到 \(t\) 的增广路，于是我们可以推断“最小割 \(=\) 最大流”。

于是我们就可直接使用 EK 或 Dinic 求最小割。

费用流

在一个网络中，每条边不止有一个容量 \(c(u, v)\)，还拥有一个给定的费用 \(w(u, v)\)。若边 \((u, v)\) 通过时流量为 \(f(u, v)\)，则花费的费用为 \(f(u, v) \times w(u, v)\)。这种网络中的最大流的最小总花费为 最小花费最大流，最大流的最大总花费为 最大花费最大流，两者统称为 费用流 模型。当然费用流的前提是最大流。

像是二分图带权最大匹配这种问题，就可使用最大费用最大流解决。

求解费用流常见使用 Edmonds-Karp 增广路算法。

Edmonds-Karp 增广路算法（EK 算法）

我们只需要在 EK 算法求最大流的算法中改动一个点即可求费用流。就是将“使用 BFS 求增广路”改为“使用 SPFA 求费用和最小的增广路”即可，即把 \(w(u, v)\) 当作边权跑最短路，找到增广路后将该路径的费用计入答案。注意由于斜对称，对于一条边的边权为 \(w(u, v)\)，我们同样要把反边的边权设为 \(w(v, u) = -w(u, v)\)。

这里列举了最小花费最大流的代码：

struct Node {
    std::vector<struct Edge> e;
    struct Edge *in;
    int f, d;
    bool q;
};

struct Edge {
    Node *s, *t;
    int c, f, w, r;

    Edge(Node *s, Node *t, int c, int w, int r) : s(s), t(t), c(c), f(0), w(w), r(r) {}
};

inline void addEdge(Node *s, Node *t, int c, int w) {
    s->e.emplace_back(s, t, c, w, t->e.size());
    t->e.emplace_back(t, s, 0, -w, s->e.size() - 1);
}

inline void ek(std::vector<Node> &nodes, int s, int t, int n, int &flow, int &cost) {
    flow = cost = 0;
    while (true) {
        for (int i = 1; i <= n; i++) {
            nodes[i].q = false;
            nodes[i].f = 0;
            nodes[i].d = INT_MAX;
            nodes[i].in = nullptr;
        }

        std::queue<Node *> q;
        q.push(&nodes[s]);
        nodes[s].f = INT_MAX, nodes[s].d = 0;

        while (!q.empty()) {
            Node *u = q.front();
            q.pop();

            u->q = false;

            for (Edge &e : u->e) {
                auto &[u, v, c, f, w, r] = e;
                if (f < c && v->d > u->d + w) {
                    v->d = u->d + w;
                    v->in = &e;
                    v->f = std::min(u->f, c - f);
                    if (!v->q) {
                        v->q = true;
                        q.push(v);
                    }
                }
            }
        }

        if (nodes[t].d == INT_MAX) return;

        for (Edge *e = nodes[t].in; e; e = e->s->in) {
            e->f += nodes[t].f;
            e->t->e[e->r].f -= nodes[t].f;
        }

        flow += nodes[t].f;
        cost += nodes[t].f * nodes[t].d;
    }
}